kiize.github.io

This is my personal page built with Quarto.

In About you can find more informations about me, in Projects you can discover what I am working on and in Gists some linux commands I find useful. Finally in Write Ups you can find a detailed explanation on some projects where I break down the problem, the methodology and the idea behind the code I have written.

Curious about what am I working on? This is a summary of my projects.

Entanglement phase transitions

In my Master’s thesis, I studied how local quantum measurements affect entanglement growth in one-dimensional fermionic systems.

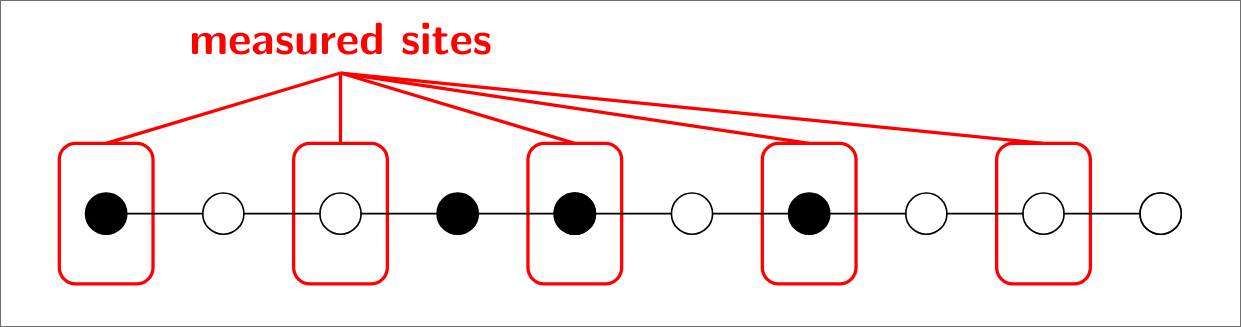
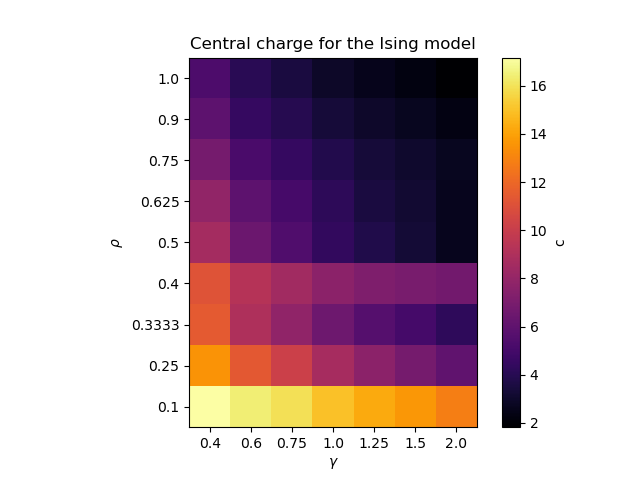
I developed a numerical framework based on stochastic Schrödinger equations and Gaussian-state formalism to simulate monitored fermionic chains. By introducing the measurement density \(\rho\) as an additional control parameter, I mapped the phase diagram of entanglement scaling and identified volume-law, logarithmic, and area-law regimes, extending known results beyond uniform monitoring.

Market crashes as critical phenomena

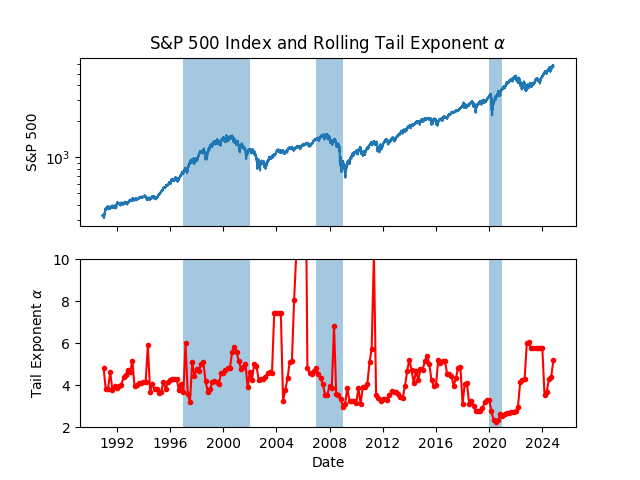
I studied financial market crashes using tools from statistical physics, analyzing the log-returns of the S&P 500 index around the 2000, 2008, and 2020 crises.

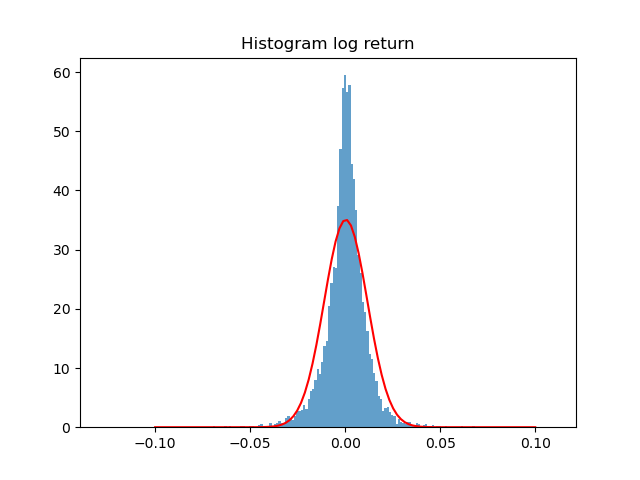
By characterizing return distributions, correlations, and volatility, I showed that market dynamics strongly deviate from Gaussian behavior and exhibit fat-tailed statistics. Using a rolling power-law analysis of return tails, I interpreted market crashes as critical-like regimes where correlations grow and extreme events become more likely, highlighting similarities between financial instability and phase transitions in physical systems.

Quantum Chaos in Billiard Systems

I studied quantum chaos through the spectral properties of quantum billiards, focusing on the transition from integrable to chaotic behavior. I implemented numerical solvers for the Helmholtz equation using both finite-difference methods and the Expansion Method, validating the approach on a rectangular billiard and extending it to the Bunimovich stadium. By unfolding the energy spectrum and analyzing level-spacing statistics, I investigated the signatures of chaos predicted by random matrix theory.

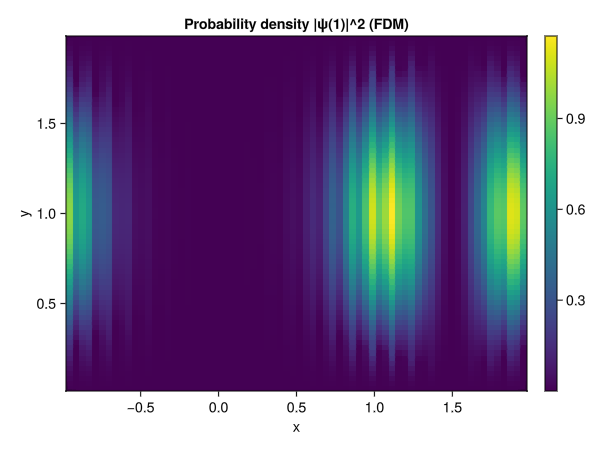
Glass transition

I investigated glassy dynamics using the two-dimensional FA Kinetically Constrained Model, implementing a Metropolis Monte Carlo simulation from scratch.

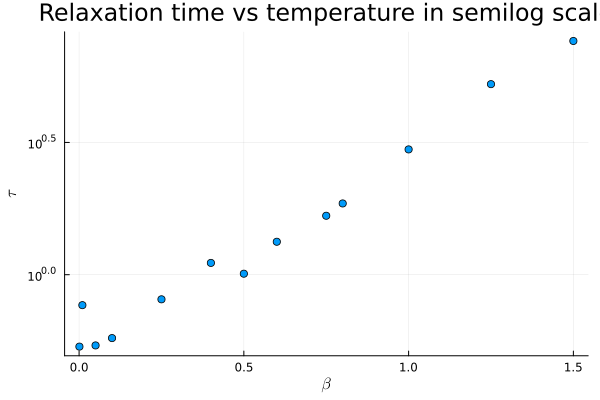
By studying the concentration of mobile regions, autocorrelation functions, and relaxation times across temperatures, I showBy studying the concentration of mobile regions, autocorrelation functions, and relaxation times across temperatures, I showed that the system does not undergo a true thermodynamic phase transition but exhibits a crossover from Arrhenius to super-Arrhenius behavior. At low temperatures, I identified the emergence of dynamic heterogeneity through spatial mobility maps, revealing the coexistence of liquid-like and solid-like regions, a key microscopic signature of glassy dynamics.ed that the system does not undergo a true thermodynamic phase transition but exhibits a crossover from Arrhenius to super-Arrhenius behavior. At low temperatures, I identified the emergence of dynamic heterogeneity through spatial mobility maps, revealing the coexistence of liquid-like and solid-like regions, a key microscopic signature of glassy dynamics.